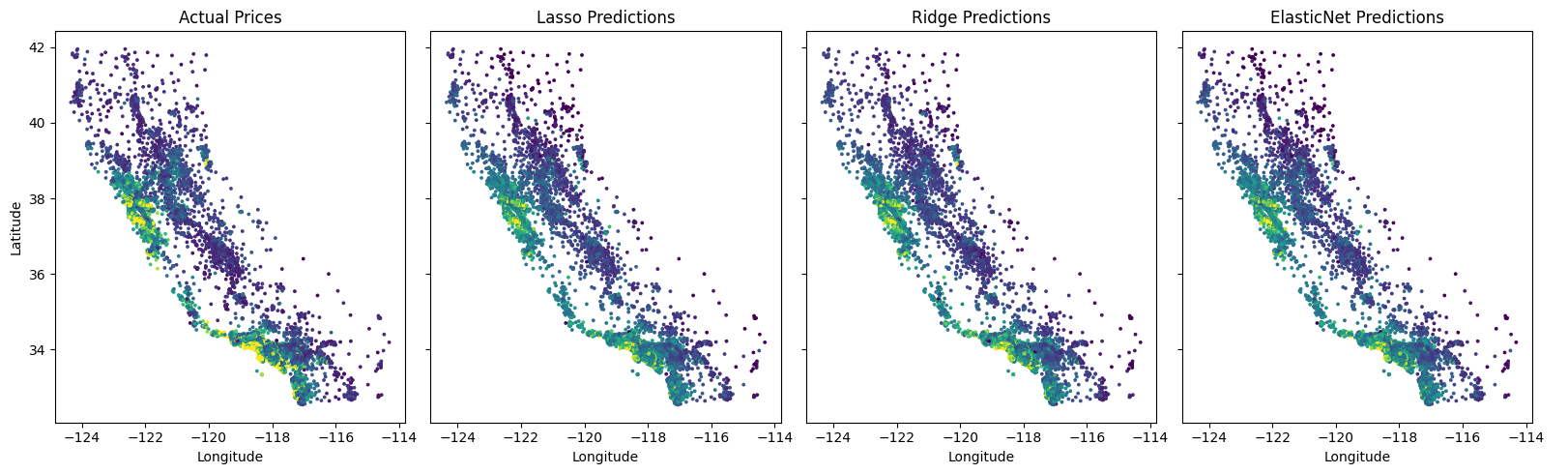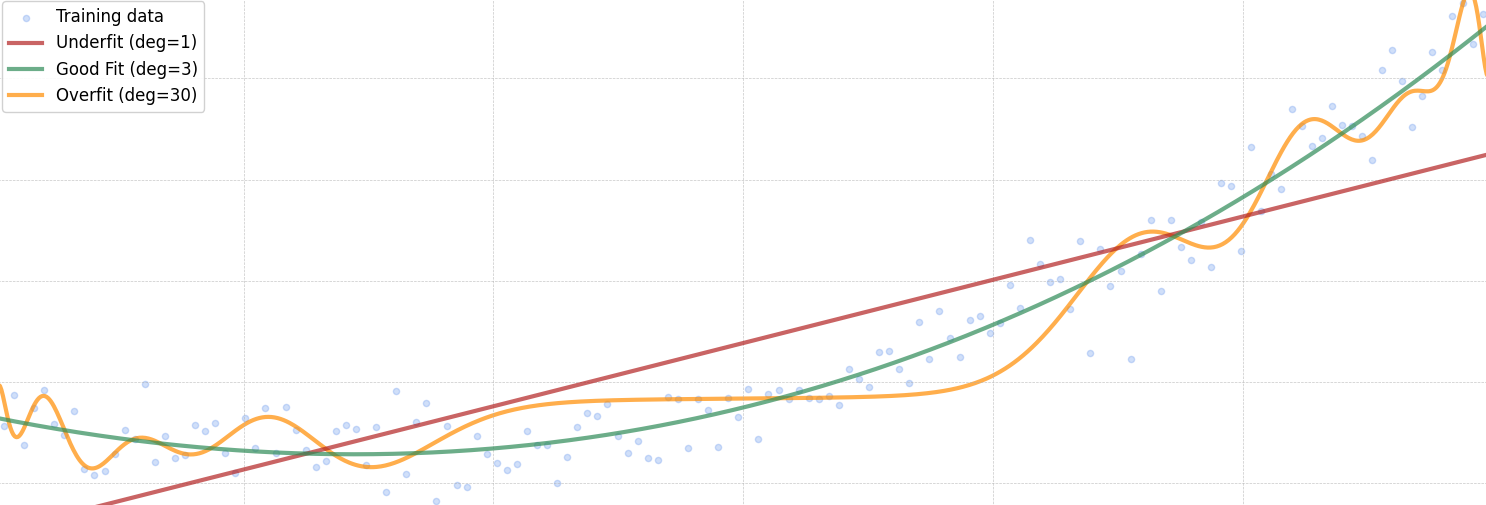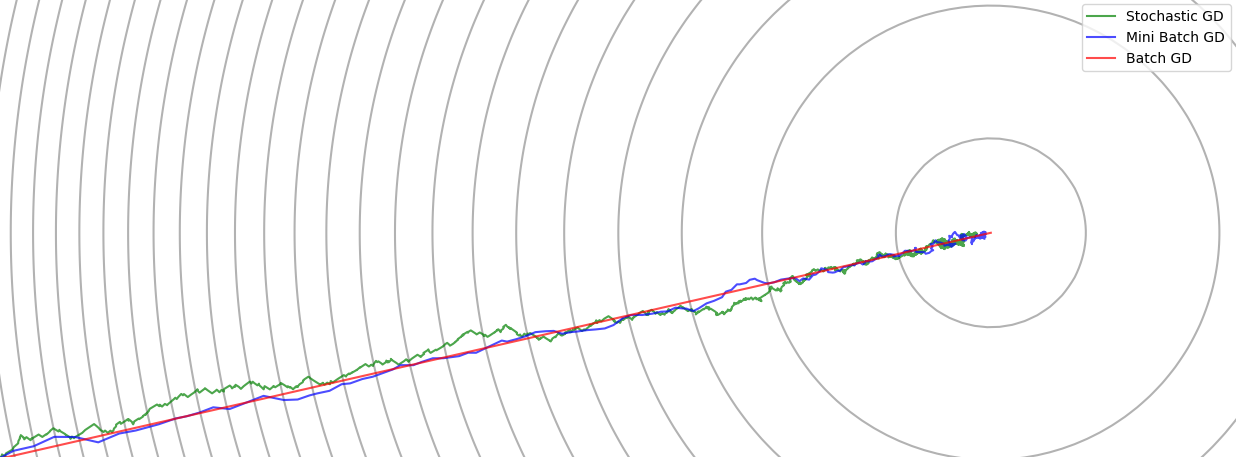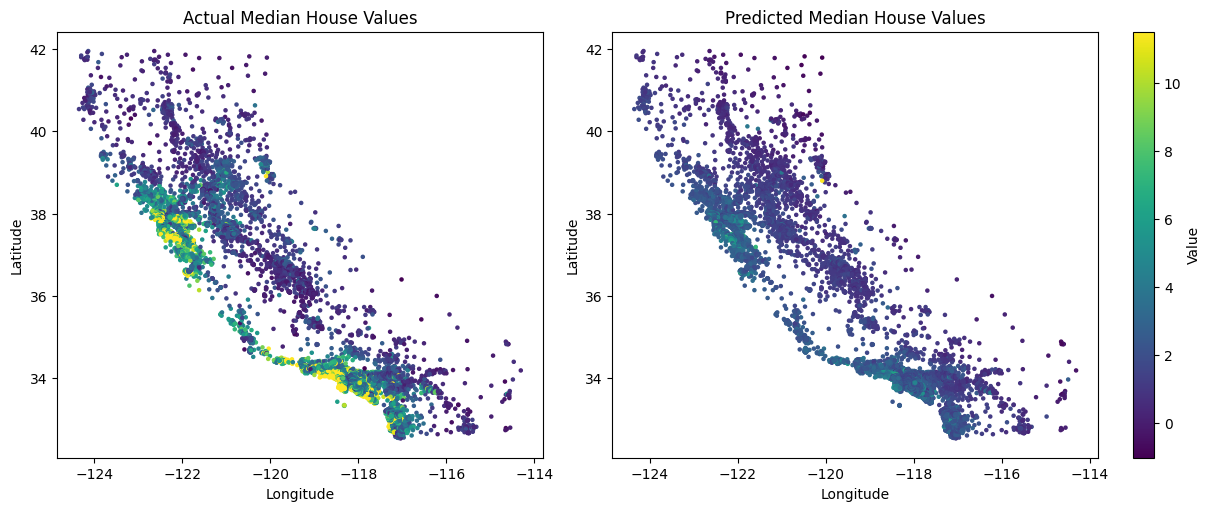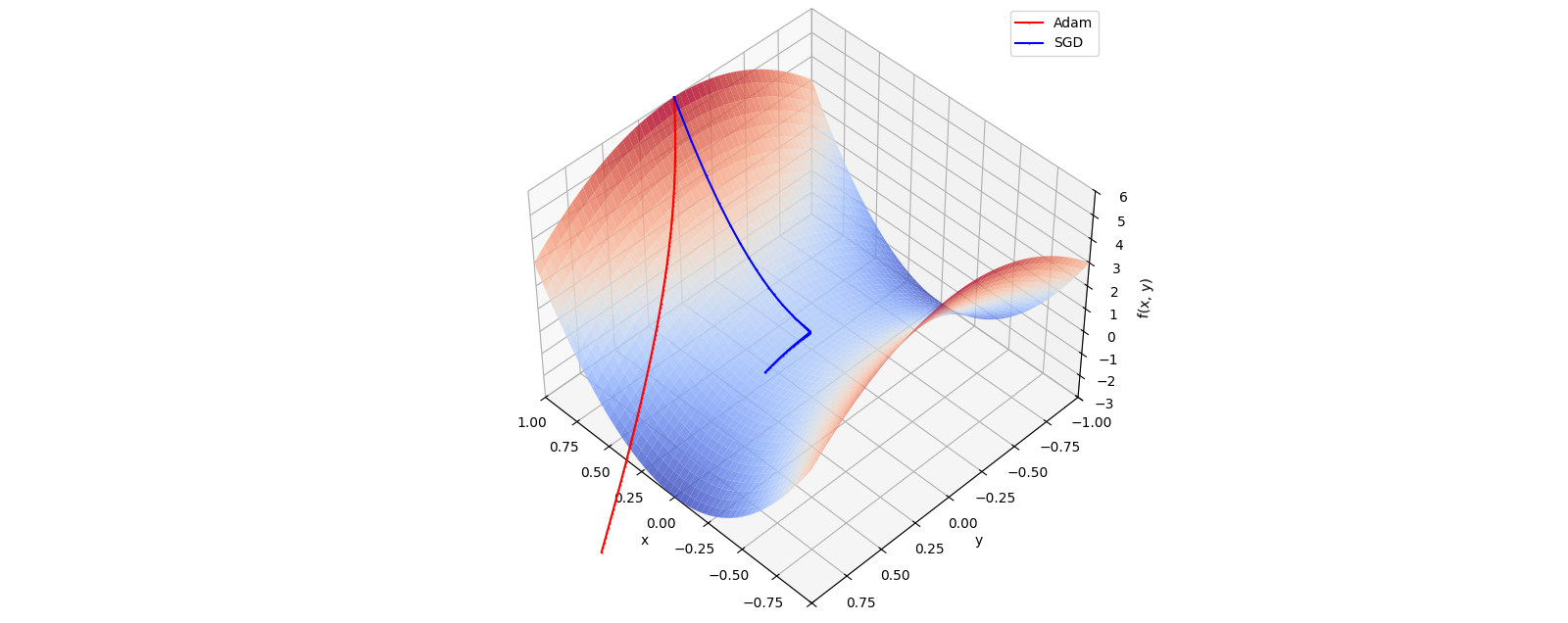
Adam Optimizer
When training deep neural networks, choosing the right optimizer can make the difference between fast, stable convergence and hours of frustration. One of the most widely used algorithms is Adam (Adaptive Moment Estimation), introduced by Diederik P. Kingma and Jimmy Ba in 2014. Adam has become the default optimizer in many frameworks (PyTorch, TensorFlow, JAX) and is still at the heart of cutting-edge models like transformers. The Idea Behind Adam Adam combines two key ideas from earlier optimizers:...