When training deep neural networks, choosing the right optimizer can make the difference between fast, stable convergence and hours of frustration. One of the most widely used algorithms is Adam (Adaptive Moment Estimation), introduced by Diederik P. Kingma and Jimmy Ba in 2014. Adam has become the default optimizer in many frameworks (PyTorch, TensorFlow, JAX) and is still at the heart of cutting-edge models like transformers.
The Idea Behind Adam
Adam combines two key ideas from earlier optimizers:
Momentum Momentum smooths the path of gradient descent by keeping a moving average of past gradients. If the slope keeps pointing in the same direction, the update accelerates (like a ball picking up speed as it rolls downhill). This reduces jitter and helps escape shallow valleys.
Adaptive step sizes (RMS scaling) Inspired by RMSProp, Adam keeps track of the average magnitude of past squared gradients. This lets it scale the learning rate per parameter:
- Large gradients → smaller step size (be cautious).
- Small gradients → larger step size (be bold).
By combining these two, Adam adapts both direction (via momentum) and step size (via RMS scaling) dynamically.
The Update Rule
At each step $t$, given the gradient $g_t$:
$$ m_t = \beta_1 m_{t-1} + (1-\beta_1) g_t $$
$$ v_t = \beta_2 v_{t-1} + (1-\beta_2) g_t^2 $$
Bias corrections (important for the early steps):
$$ \hat{m}_t = \frac{m_t}{1-\beta_1^t}, \quad \hat{v}_t = \frac{v_t}{1-\beta_2^t} $$
Parameter update:
$$ \theta_{t+1} = \theta_t - \alpha \frac{\hat{m}_t}{\sqrt{\hat{v}_t} + \varepsilon} $$
Defaults: $\alpha = 0.001, \beta_1 = 0.9, \beta_2 = 0.999, \varepsilon = 10^{-8}$.
Intuition Recap
- Momentum ($m_t$): If gradients keep pointing in the same direction, accelerate.
- RMS scaling ($v_t$): If gradients have been large, slow down; if they’ve been small, speed up.
- Bias correction: Prevents the early averages (which start at zero) from underestimating the true signal.
Adam vs. SDG
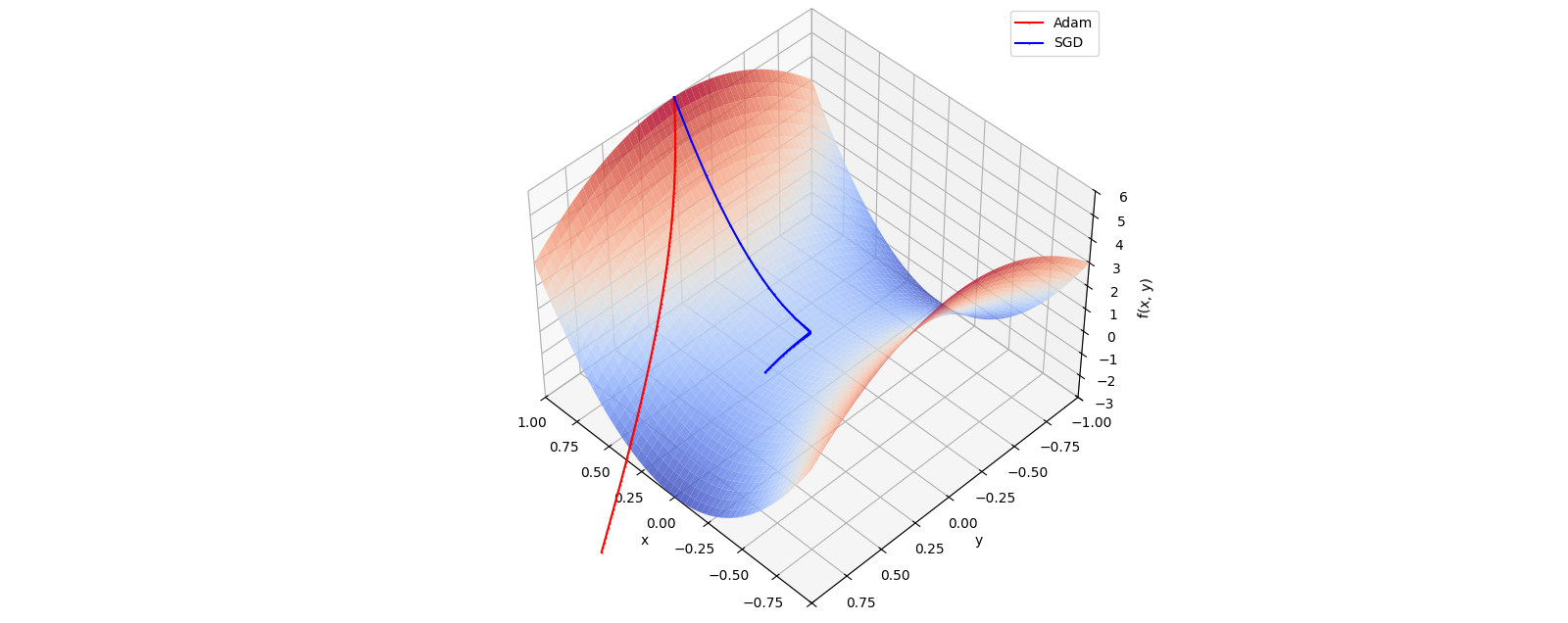
Let’s compare Adam with stochastic gradient descent (SDG). The 3D plot shows the Rosenbrock function’s characteristic banana-shaped valley as a surface. The optimization trajectories are overlaid above the surface for clarity. The Adam optimizer (red) quickly moves along the valley and reaches the minimum first, demonstrating its fast convergence in this setup. The SGD optimizer (green) progresses more gradually, following a smoother path toward the minimum but taking longer to converge.
See my Github for the Code.
Limitations of Adam
Adam isn’t perfect:
Generalization gap On tasks like image classification, Adam often converges faster than SGD but to sharper minima, leading to worse test accuracy.
Non-convergence in theory The original Adam can fail to converge in certain convex problems. Variants like AMSGrad fix this.
Weight decay issue L2 regularization (weight decay) doesn’t behave properly in Adam, since the penalty term is scaled by the adaptive learning rate. The AdamW variant decouples weight decay, making it the optimizer of choice in modern NLP.
Reference
- D. P. Kingma and J. Ba. Adam: A Method for Stochastic Optimization. 2014. arXiv:1412.6980